Many people quote the universal approximation theorem as a reason why neural networks are sucessful. While it’s cool that neural networks can approximate arbitrary continuous multivariate functions, the universal approximation theorem has some flaws:

• In general, it does not tell you what “approximation” means.
• Given some notion of approximation, it does not even tell you how to arrive at that approximation, just that it exists.

I claim that we can solve both of these problems in a huge way by switching from neural networks to bands of elephants. Not only can the band of elephants represent the function exactly instead of approximating it, we can even construct that band of elephants given the function. To be precise, for a function f : [0, 1]ⁿ → ℝ, we’ll recruit (2n + 1) ⋅ n elephants. The elephants are distributed across 2n + 1 rooms equipped with microphones, and there is a mixing room where the rooms’ audio signals are mixed into a single output.

From the Kolmogorov–Arnold representation theorem, we get that every continuous multivariate function f : [0, 1]ⁿ → ℝ is representable as

where ϕ_q, p : [0, 1] → ℝ and Φ_q : ℝ → ℝ.

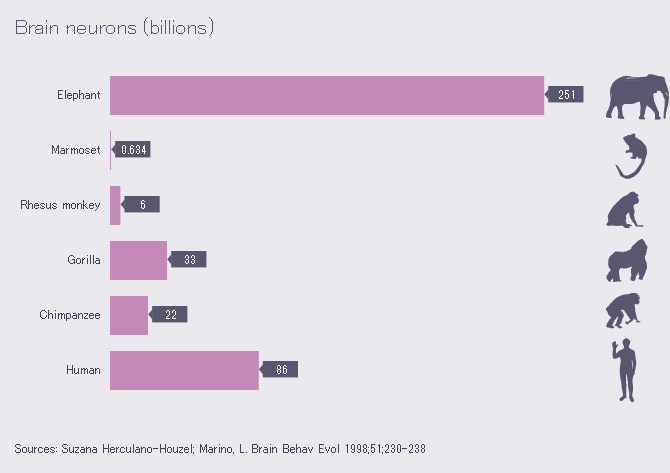
We’ll assign the function ϕ_q, p to the pth elephant in room q. The mixing elephant will mix each incoming value to the one dictated by Φ_q. To get an output from this system, we’ll have every pth elephant trumpet according to the input x_p and their personal instructions, let the mixing elephant mix the signals, and then look at the output. While the instructions for the elephants may become complex, this is no problem as elephants have great memory and are very intelligent. Indeed, they have 251 billion neurons, while we humans have a measly 86 billion:

Teaching the elephants should be no problem either. Elephants learn sounds from each other and can even imitate truck and bird sounds.

Let’s talk about the inference speed of this setup. As the elephants produce sound waves, and assuming they all trumpet at the same frequency, we need to wait until the wave peaks until we know the amplitude of the signal. According to one paper, the highest an elephant can trumpet is around 5879 Hz. As we only need to wait for one quarter cycle, our inference speed at this frequency would be about 425 microseconds. While this might not be a great showing compared to some neural networks, at least the problem gets solved correctly.

One problem you might want to think about is elephant upkeep. Let’s compare this to large language model training cost. According to a shady AI website, GPT-4 cost about 63 million dollars to train. To compare this to our elephant’s costs, we need to formulate GPT-4 as an n-ary continuous function. Suppose that GPT-4 lives in a 3072-dimensional space and has a maximum context window of 128000 tokens, we need n = 393216000 inputs, and thus we need 3.09 ⋅ 10¹⁷ elephants. According to the PAWS performing animal welfare society, the upkeep of an elephant costs 100,000 dollars a year, giving us a yearly expense of about 30 sextillion dollars. Let’s see if I find some money to fund it.